
题目列表(包括答案和解析)
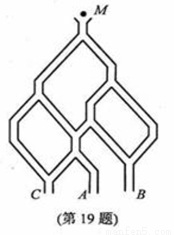
(19) (本题满分l4分)如图,一个小球从M处投入,通过管道自
 上而下落A或B或C。已知小球从每个叉口落入左右两个
上而下落A或B或C。已知小球从每个叉口落入左右两个
管道的可能性是相等的.
某商家按上述投球方式进行促销活动,若投入的小球落
到A,B,C,则分别设为l,2,3等奖.
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量 的分布列及期望
的分布列及期望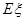 ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量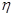 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求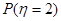 .
.
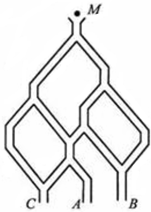 如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.
如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.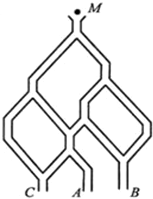 如图,一个小球从M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
 (I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量![]() 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量![]() 的分布列及期望
的分布列及期望![]() ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量![]() 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求![]() .
.
(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
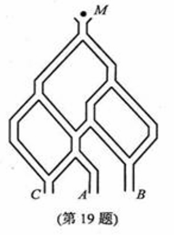 (I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量![]() 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量![]() 的分布列及期望
的分布列及期望![]() ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量![]() 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com