某次运动会甲、乙两名射击运动员成绩如下：

甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；

乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；

（1）用茎叶图表示甲，乙两个成绩；

（2）分别计算两个样本的平均数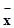和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定．

本小题满分12分）
某次运动会甲、乙两名射击运动员成绩如下：
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；
（1）用茎叶图表示甲，乙两个成绩；
（2）分别计算两个样本的平均数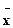和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定。

某次运动会甲、乙两名射击运动员成绩如下：
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；
（1）用茎叶图表示甲，乙两个成绩；
（2）根据茎叶图分析甲、乙两人成绩；
（3）分别计算两个样本的平均数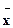和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定.

在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩：

甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；

乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；

（1）用茎叶图表示甲，乙两个成绩；并根据茎叶图分析甲、乙两人成绩；

（2）分别计算两个样本的平均数和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定。