
题目列表(包括答案和解析)
给出以下四个命题:
①动点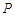 到两定点
到两定点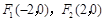 的距离之和为4,则点
的距离之和为4,则点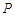 的轨迹为椭圆;
的轨迹为椭圆;
②设定义在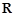 上的可导函数
上的可导函数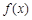 满足
满足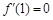 ,
, ,则
,则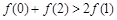 一定成立;
一定成立;
③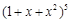 展开式中,含
展开式中,含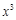 项的系数为30;
项的系数为30;
④若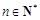 ,则
,则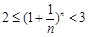 .
.
其中,所有真命题的序号为 .
 到两定点
到两定点 的距离之和为4,则点
的距离之和为4,则点 的轨迹为椭圆;
的轨迹为椭圆; 上的可导函数
上的可导函数 满足
满足 ,
, ,则
,则 一定成立;
一定成立; 展开式中,含
展开式中,含 项的系数为30;
项的系数为30; ,则
,则 .
.| 2 |
| 3 |
| I1 |
| I2 |
定义集合![]() 与
与![]() 的差集
的差集![]() 。记“从集合
。记“从集合![]() 中任取一个元素
中任取一个元素![]() ”为事件
”为事件![]() ,“从集合
,“从集合![]() 中任取一个元素
中任取一个元素![]() ”为事件
”为事件![]() ;
;![]() 为事件
为事件![]() 发生的概率,
发生的概率,![]() 为事件
为事件![]() 发生的概率。当
发生的概率。当![]() ,且
,且![]() 时,设集合
时,设集合![]() ,集合
,集合![]() 。给出下列判断: ①当
。给出下列判断: ①当![]() 时,
时,![]() ;②总有
;②总有![]() ;③若
;③若![]() ,则
,则![]() ;④
;④![]() 不可能等于1。其中所有判断正确的序号是 。
不可能等于1。其中所有判断正确的序号是 。
矩形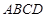 的中心在坐标原点,边
的中心在坐标原点,边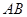 与
与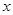 轴平行,
轴平行,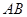 =8,
=8,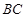 =6.
=6.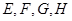 分别是矩形四条边的中点,
分别是矩形四条边的中点,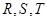 是线段
是线段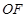 的四等分点,
的四等分点,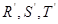 是线段
是线段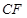 的四等分点.设直线
的四等分点.设直线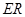 与
与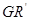 ,
,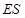 与
与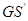 ,
,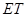 与
与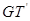 的交点依次为
的交点依次为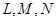 .
.
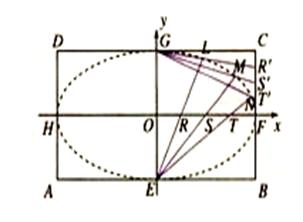
(1)求以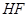 为长轴,以
为长轴,以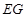 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点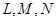 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段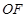 的
的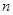 (
(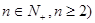 等分点从左向右依次为
等分点从左向右依次为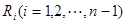 ,线段
,线段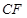 的
的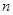 等分点从上向下依次为
等分点从上向下依次为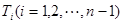 ,那么直线
,那么直线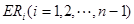 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com