
题目列表(包括答案和解析)
在一次气象调查中,发现某城市的温度θ℃近似地按照规则θ=25+6sin![]() t在波动,其中t(h)是从某日9∶00开始计算的时间,且t≤24.
t在波动,其中t(h)是从某日9∶00开始计算的时间,且t≤24.
(1)画出温度随时间波动的图象;
(2)利用函数图象确定最高温度和最低温度;
(3)最高温度和最低温度在什么时候出现?
(4)在什么时候温度为①27℃?②20℃?
利用函数图像比较大小:
(1)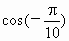 与
与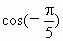 ;(2)
;(2)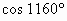 与
与
![]() .
.
利用函数图像可判断函数
f(x)=lnx+2x-6的零点个数为[
]|
A .0 |
B .1 |
C .2 |
D .3 |
利用函数图像判断下列方程有没有根,有几个根:
|
(1) |
(2) |
|
(3) |
(4) |
某简谐运动得到形如![]() 的关系式,其中:振幅为4,周期为6π,初相为
的关系式,其中:振幅为4,周期为6π,初相为![]() ;
;
(Ⅰ)写出这个函数的关系式;
(Ⅱ)用五点作图法作出这个函数在一个周期内的图象.

(Ⅲ)说明这个函数图像可由y=sinx的图象经过怎样的变换得到.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com