练习册

  • 练习册
  • 试题
    ＝-2(|x|-)2+≤.22．已知f(x)是二次函数.不等式f(x)<0的解集是(0,5).且f(x)在区间[-1,4]上的最大值是12. (1)求f(x)的解析式． (2)是否存在自然数m.使得方程f(x)+＝0在区间 (m.m+1)内有且只有两个不等的实数根?若存在.求出所有m的值,若不存在.请说明理由． 解:(1)∵f(x)是二次函数.且f(x)<0的解集是(0,5).∴可设f(x)＝ax(x-5)(a>0)． ∴f(x)在区间[-1,4]上的最大值是f(-1)＝6a.由已知.得6a＝12.∴a＝2. ∴f(x)＝2x(x-5)＝2x2-10x(x∈R)． (2)方程f(x)+＝0等价于方程2x3-10x2+37＝0. 设h(x)＝2x3-10x2+37. 则h′(x)＝6x2-20x＝2x(3x-10)． 当x∈(0.)时.h′(x)<0.h(x)是减函数, 当x∈时.h′(x)>0.h(x)是增函数． ∵h(3)＝1>0.h()＝-<0.h(4)＝5>0. ∴方程h(x)＝0在区间内分别有唯一实数根. 而在区间内没有实数根． ∴存在唯一的自然数m＝3.使得方程f(x)+＝0在区间(m.m+1)内有且只有两个不同的实数根． 【查看更多】

     

    题目列表(包括答案和解析)

    下列四个命题中，正确的是（　　）
    A、通过点（0，2）且倾斜角是15°的直线方程是y=(
    		3
    -2)x+2
    B、设直线l1和l2的斜率分别为k1和k2，则l1和l2的夹角是θ=arctg
    k2-k1
    1+k1•k2
    C、直线x+
    		2
    y-1=0    的倾斜角是arctg(-
    		2
    2
    )
    D、已知三点A（a+b，c），B（b+c，a），C（c+a，b），则A，B，C三点共线

    查看答案和解析>>

    下列四个命题中，正确的是（　　）
    A．通过点（0，2）且倾斜角是15°的直线方程是y=(
    		3
    -2)x+2
    B．设直线l1和l2的斜率分别为k1和k2，则l1和l2的夹角是θ=arctg
    k2-k1
    1+k1•k2
    C．直线x+
    		2
    y-1=0    的倾斜角是arctg(-
    		2
    2
    )
    D．已知三点A（a+b，c），B（b+c，a），C（c+a，b），则A，B，C三点共线

    查看答案和解析>>

    (2005山东，22)如下图,已知动圆过定点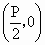，且与直线相切，其中p＞0，

    (1)求动圆圆心的轨迹C的方程；

    (2)设A、B是轨迹C上异于原点O的两个不同点，直线OA和OB的倾斜角分别为α和β，当α、β变化且α+β为定值θ(0＜θ＜π)时，证明：直线AB恒过定点，并求出该定点的坐标．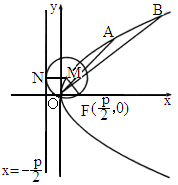

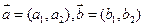    查看答案和解析>>

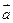
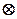
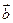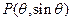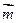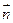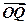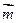
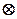
    设，定义一种向量积：＝(a1b1，a2b2)．已知点，＝，＝，点Q在y＝f(x)的图象上运动，满足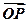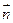＝＋ (其中O为坐标原点)，则y＝f(x)的最大值A及最小正周期T分别为   (　　)
    A．2，πB．2,4πC．，4πD．，π

    查看答案和解析>>

    下列四个命题：

    ① 的展开式共有6项；

    ②设回归直线方程为＝2－2．5x，当变量x增加—个单位时，y平均增加2．5个单位；

    ③已知ξ服从正态分布N （0，），且P（－2≤ξ≤0）＝0．4，则P（ξ＞2）＝0．2；

    ④已知函数f（a）＝，则f[f（）]＝1－cos1．其中正确命题的个数为

       （A）4          （B）3             （C）2            （D）1

     

    查看答案和解析>>


    同步练习册答案