
题目列表(包括答案和解析)
(本题满分14分)已知![]() ,
,![]() ,
,
(1)若f(x)在![]() 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
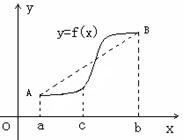
 (2)如右图所示,若函数
(2)如右图所示,若函数![]() 的图象在
的图象在![]() 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在![]() 使得
使得![]() ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
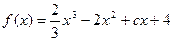 ,
,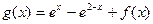 ,
,
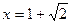 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;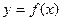 的图象在
的图象在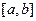 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在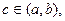 使得
使得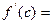 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)(本小题满分14分)
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列![]() 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列![]() ,满足
,满足![]()
![]() .
.
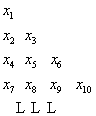 (Ⅰ)证明数列
(Ⅰ)证明数列![]() 是等比数列;
是等比数列;
(Ⅱ)把数列![]() 中所有项按如图所示的规律排成一个三角形
中所有项按如图所示的规律排成一个三角形
数表,当![]() 时,求第
时,求第![]() 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列![]() ,证明:
,证明:![]() .
.
(本小题满分14分)
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列![]() 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列![]() ,满足
,满足![]()
![]() .
.
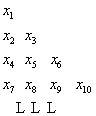 (Ⅰ)证明数列
(Ⅰ)证明数列![]() 是等比数列;
是等比数列;
(Ⅱ)把数列![]() 中所有项按如图所示的规律排成一个三角形
中所有项按如图所示的规律排成一个三角形
数表,当![]() 时,求第
时,求第![]() 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列![]() ,证明:
,证明:![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com