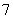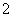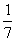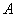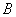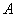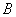（本题满分１4分） 袋中有分别写着“团团”和“圆圆”的两种玩具共个且形状完全相同，从中任取个玩具都是“圆圆”的概率为，、两人不放回从袋中轮流摸取一个玩具，先取，后取，然后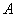再取，……直到两人中有一人取到“圆圆”时即停止游戏．每个玩具在每一次被取出的机会是均等的，用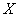表示游戏终止时取玩具的次数．

   （1）求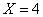时的概率；

   （2）求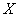的数学期望．

袋中有分别写着“团团”和“圆圆”的两种玩具共个且形状完全相同，从中任取个玩具都是“圆圆”的概率为，、两人不放回从袋中轮流摸取一个玩具，先取，后取，然后再取，……直到两人中有一人取到“圆圆”时即停止游戏．每个玩具在每一次被取出的机会是均等的，用表示游戏终止时取玩具的次数．

   （1）求时的概率；[来源:Zxxk.Com]

   （2）求的数学期望．

（本小题满分12分）袋中有分别写着“团团”和“圆圆”的两种玩具共7个，且形状完全相同，从中任取2个玩具都是“圆圆”的概率为，A、B两人不放回从袋中轮流摸取一个玩具，A先取，B后取，然后A再取，……直到两人中有一人取到“圆圆”时即停止游戏，每个玩具在每一次被取出的机会是均等的，用表示游戏终止时取玩具的次数。 （1）求袋中“圆圆”的个数；  （2）求3的概率。