
题目列表(包括答案和解析)
两个平面同时垂直于一条直线,则两个平面平行.
已知:α、β是两个平面,直线
l⊥α,l⊥β,垂足分别为A、B.求证:α∥β思路1:根据判定定理证.
给出下列命题:
①若平面α内有无数个点到平面β的距离相等,则α∥β;
②若平面α内有不共线三点到平面β的距离相等,则α∥β;
③平行于同一条直线的两个平面平行;
④垂直于同一条直线的两个平面平行;
⑤若在空间内存在两条异面直线同时平行于两个平面,则这两个平面平行.
其中所有正确命题的序号为________.
给出下列命题
A.一直线与一个平面内的无数条直线垂直,则此直线与平面垂直;
B.两条异面直线不能同时垂直于一个平面;
C.直线倾斜角的取值范围是:0°<![]() ≤180°;
≤180°;
D.两异面直线所成的角的取值范围是:0°<![]() <90°;
<90°;
E.正弦函数在第一象限内为增函数;
F.y=sin2x的图像关于点(![]() ,0)对称.其中正确的是________(写出所有正确的序号).
,0)对称.其中正确的是________(写出所有正确的序号).
| A.一直线与一个平面内的无数条直线垂直,则此直线与平面垂直; |
| B.两条异面直线不能同时垂直于一个平面; |
C.直线倾斜角的取值范围是: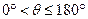 ; ; |
D.两异面直线所成的角的取值范围是: . . |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com