
题目列表(包括答案和解析)
(2009全国卷Ⅱ文)(本小题满分12分)
|
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有![]() 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
(2009全国卷Ⅱ文)(本小题满分12分)
|
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有![]() 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
平面直角坐标系内的向量都可以用一有序实数对唯一表示,这使我们想到可以用向量作为解析几何的研究工具.如图,设直线
l的倾斜角为α(α≠90°).在l上任取两个不同的点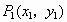 ,
, ,不妨设向量
,不妨设向量 的方向是向上的,那么向量
的方向是向上的,那么向量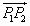 的坐标是(
的坐标是( ).过原点作向量
).过原点作向量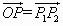 ,则点P的坐标是(
,则点P的坐标是( ),而且直线OP的倾斜角也是α.根据正切函数的定义得
),而且直线OP的倾斜角也是α.根据正切函数的定义得
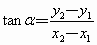 ,
,
这就是《数学
2》中已经得到的斜率公式.上述推导过程比《数学2》中的推导简捷.你能用向量作为工具讨论一下直线的有关问题吗?例如:(1)
过点 ,平行于向量
,平行于向量 的直线方程;
的直线方程;
(2)
向量(A,B)与直线 的关系;
的关系;
(3)
设直线 和
和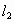 的方程分别是
的方程分别是
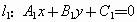
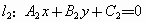
那么,
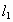 ∥
∥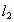 ,
,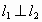 的条件各是什么?如果它们相交,如何得到它们的夹角公式?
的条件各是什么?如果它们相交,如何得到它们的夹角公式?
(4)
点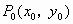 到直线
到直线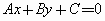 的距离公式如何推导?
的距离公式如何推导?
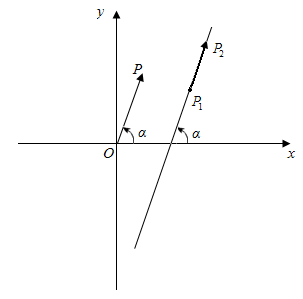
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com