如图.在直三棱柱ABC- A1B1C1中.AC＝BC＝CC1＝2.AC⊥BC.D为AB的中点. (1)求证:AC1∥平面B1CD, (2)求二面角B-B1C-D的正弦值. 解:(1)证明:如图.连接BC1交B1C于点E. 则E为BC1的中点. ∵D为AB的中点.∴在△ABC1中.AC1∥DE 又AC1⊄平面B1CD.DE⊂平面B1CD. ∴AC1∥平面B1CD (2)∵AC＝BC.D为AB的中点. ∴CD⊥AB.又平面ABC⊥平面ABB1A1. ∴CD⊥平面ABB1A1. ∴平面B1CD⊥平面B1BD. 过点B作BH⊥B1D.垂足为H.则BH⊥平面B1CD. 连接EH. ∵B1C⊥BE.B1C⊥EH. ∴∠BEH为二面角B-B1C-D的平面角. 在Rt△BHE中.BE＝.BH＝＝. 则sin∠BEH＝＝. 即二面角B-B1C-D的正弦值为. 【
查看更多】
题目列表(包括答案和解析)
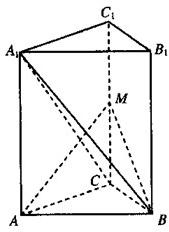
如图，在直三棱柱ABC-A
1B
1C
1中，
∠ACB=90°，CB=1，CA=，AA1=，M为侧棱CC
1上一点，AM⊥BA
1．
（Ⅰ）求证：AM⊥平面A
1BC；
（Ⅱ）求二面角B-AM-C的大小．
查看答案和解析>>
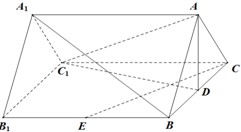
如图，在直三棱柱ABC-A
1B
1C
1中，AB=AC=5，D，E分别为BC，BB
1的中点，四边形B
1BCC
1是边长为6的正方形．
（Ⅰ）求证：A
1B∥平面AC
1D；
（Ⅱ）求证：平面A
1CE⊥平面AC
1D．
查看答案和解析>>
如图，在直三棱柱ABC-A
1B
1C
1中，AC=BC=2，AB=AA
1=
2，点D是AB的中点，点E是BB
1的中点．
（1）求证：A
1B⊥平面CDE；
（2）求二面角D-CE-A
1的大小．
查看答案和解析>>
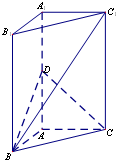
如图，在直三棱柱ABC-A
1B
1C
1中，
AB⊥AC，AB=AC=AA1，D是AA
1的中点，则BC
1与平面BCD所成的角正弦值为（ ）
查看答案和解析>>
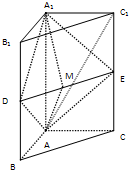
如图，在直三棱柱ABC-A
1B
1C
1中，AB⊥AC，AB=AC=1，AA
1=2，D、E分别是BB
1、CC
1的中点，M是DE的中点．
（1）求证：平面ADE⊥平面AMA
1；
（2）试问能否在线段AC
1上找一点N，使得直线MN与平面ADA
1平行？请说明理由；
（3）求三棱锥A
1-ADE的体积．
查看答案和解析>>
