
题目列表(包括答案和解析)
 已知椭圆
已知椭圆| x2 |
| 8 |
| y2 |
| 2 |
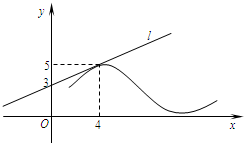 如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=
如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=| 1 |
| 2 |
| 1 |
| 2 |
 (2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足
(2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足| MA |
| MB |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
| p |
| 2 |
| p |
| 2 |
| QP |
| QF |
| FP |
| FQ |
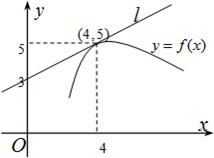 如图,直线l是曲线y=f(x)在(4,5)处的切线,则f′(4)=
如图,直线l是曲线y=f(x)在(4,5)处的切线,则f′(4)=| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com