
题目列表(包括答案和解析)
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
A.
| B.7 |
下列人类所需的营养物质中,既不参与构成人体细胞,也不为人体提供能量的是,答案:0,选项:维生素,选项:水,选项:无机盐,... - 初中生物 - 精英家教网
.artpreview dt{background:#fff;color:#000}#cont{background:#fff url(http://img.jyeoo.net/images/body_bg.jpg) repeat-x;margin:0}
function initJavaScriptCallback() { QuesCart.init("bio", true); }
var imageRootUrl="http://img.jyeoo.net/",wwwRootUrl="http://www.jyeoo.com/",blogRootUrl="http://blog.jyeoo.com/",spaceRootUrl="http://space.jyeoo.com/",loginUrl="http://www.jyeoo.com/",logoutUrl="http://www.jyeoo.com/account/logoff",scriptsUrl="http://img.jyeoo.net/scripts/",isMobile=false;var mustyleAttr={color:"#000000",fontsize:"13px",fontfamily:"arial",displaystyle:"true"};document.domain="jyeoo.com";$.ajaxSetup({cache:true});C.-
| D.-
|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
initJavaScript();
充值|设为首页|免费注册|登录
 在线问答在线组卷在线训练 精英家教网 更多试题 》试题下列人类所需的营养物质中,既不参与构成人体细胞,也不为人体提供能量的是( )
故选:A点评:解答此题的关键是熟练掌握人体需要的营养物质及其作用.答题:xushifeng老师 隐藏解析在线训练 |
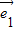 和
和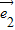 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 ,则存在唯一的一对实数λ,μ,使得
,则存在唯一的一对实数λ,μ,使得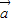 =
=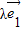 +μ
+μ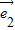 ,我们就把实数对(λ,μ)称作向量
,我们就把实数对(λ,μ)称作向量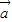 的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用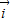 和
和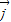 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<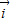 ,
,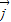 >=
>=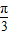 ,
, 和
和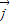 做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量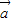 的坐标;
的坐标;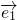 和
和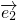 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 ,则存在唯一的一对实数λ,μ,使得
,则存在唯一的一对实数λ,μ,使得 =
=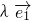 +μ
+μ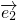 ,我们就把实数对(λ,μ)称作向量
,我们就把实数对(λ,μ)称作向量 的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用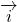 和
和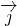 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<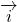 ,
,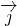 >=
>= ,
,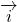 和
和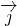 做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量 的坐标;
的坐标;| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com