练习册

  • 练习册
  • 试题
    16． 如图.在中.是上的高.沿把折起.使 . (Ⅰ)证明:平面ADB ⊥平面BDC, (Ⅱ )设E为BC的中点.求与 夹角的余弦值. 解(Ⅰ)∵折起前AD是BC边上的高. ∴ 当Δ ABD折起后.AD⊥DC.AD⊥DB. 又DBDC＝D. ∴AD⊥平面BDC. ∵AD 平面平面BDC. (Ⅱ )由∠ BDC＝及(Ⅰ)知DA.DB.DC两两垂直.不防设=1.以D为坐标原点.以..所在直线轴建立如图所示的空间直角坐标系.易得D.C.A(0,0.).E(..0). =. =. 与夹角的余弦值为 ＜.＞=. 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)如图，在△ABC中，∠ABC=45°，∠BAC=90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC=90°。

    （1）证明：平面ＡＤＢ⊥平面ＢＤＣ；

    （2 ）设BD=1，求三棱锥D—ＡＢＣ的表面积。

     

     

     

     

     

     

     

    查看答案和解析>>

    (本小题满分12分)

    如图，在三棱锥P-ABC中，⊿PAB是等边三角形，D，E分别为AB，PC的中点.

    （Ⅰ）在BC边上是否存在一点F，使得PB∥平面DEF.

    （Ⅱ）若∠PAC=∠PBC=90º，证明：AB⊥PC

    查看答案和解析>>

    (本小题满分12分)如图，在△ABC中，∠ABC=45°，∠BAC=90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC=90°。
    （1）证明：平面ＡＤＢ⊥平面ＢＤＣ；
    （2 ）设BD=1，求三棱锥D—ＡＢＣ的表面积。
     

    查看答案和解析>>

    (本小题满分12分)如图，在四棱锥P—ABCD中，底面ABCD是正方形，PA⊥底面ABCD，且PA=AB，M、N分别是PA、BC的中点．
    (I)求证：MN∥平面PCD；
    (II)在棱PC上是否存在点E，使得AE上平面PBD?若存在，求出AE与平面PBC所成角的正弦值，若不存在，请说明理由

    查看答案和解析>>

    (本小题满分12分)

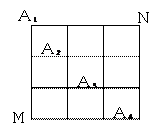
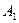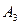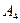    如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网，、、、是道路网中位于一条对角线上的４个交汇处，今甲由道路网Ｍ处出发随机地选择一条沿街的最短路径到达Ｎ处.
    （Ⅰ）求甲由M处到达N处的不同走法种数；
    （Ⅱ）求甲经过的概率.

    查看答案和解析>>


    同步练习册答案