
题目列表(包括答案和解析)
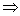 m⊥n; ②m⊥n
m⊥n; ②m⊥n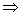 m1⊥n1;
m1⊥n1; m与n相交或重台;④m1与n1平行
m与n相交或重台;④m1与n1平行 m与n平行或重合;
m与n平行或重合;  某食品厂为了检查甲乙两条自动包装流水线的生产情况,在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.| 产品重量(克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
| A、P与R互斥 | B、Q与R互斥 | C、任何两个都互斥 | D、任何两个均不互斥 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com