有三个连续的自然数，它们都小于2008，其中最小的能被13整除，中间的能被15整除，最大的能被17整除．那么这三个自然数中最小的一个是多少？

27、有三个连续的自然数，中间一个是x，则它们的积是．

有三个连续的自然数，中间一个是x，则它们的积是______．

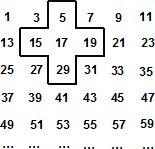
将连续的奇数1，3，5，7，…，排成如下图的数表，用图中所示的十字框可任意框出5个数．
【探究规律一】：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为．
【结论】：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是．
【探究规律二】：落在十字框中间且又是第二列的奇数是15，27，39，51…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列的奇数分别可表示为．
【运用规律】：
（1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是；这个奇数落在从左往右第列．
（2）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．