化简：
（1）-5aⁿ-aⁿ-（-7aⁿ）+（-3aⁿ）
（2）x²y-3xy²+2yx²-y²x
（3）

1

4

a2b-0.4ab2-

1

2

a2b+

2

5

ab2；
（4）3a-{2c-[6a-（c-b）+c+（a+8b-6）]}．

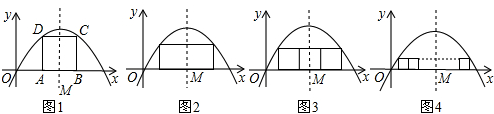
阅读：如图（1），正方形ABCD的边AB在x轴上，C、D在抛物线y=-x（x-2）的图象上，我们称正方形ABCD内接于抛物线y=-x（x-2）．抛物线y=-x（x-2）的对称轴交x轴于点M，设正方形ABCD的边长为a₁，那么a₁满足哪个二元一次方程呢？由对称性可知M是AB的中点，则AM=

1

2

a1，AD=a₁．易知OM=1，所以OA=1-

1

2

a1，所以D点坐标为(1-

1

2

a1，a1)，代入抛物线解析式并化简可知a₁满足二元一次方程(

1

2

)2a12+a1-1=0；根据以上材料探索：（第（1）小题要求写出过程，其它两小题只要写出答案，不必要过程）
（1）如图（2），若并排两个正方形内接于抛物线y=-x（x-2），则每个正方形的边长a₂满足的二元一次方程是；
（2）如图（3），若并排三个正方形内接于抛物线y=-x（x-2），则每个正方形的边长a₃满足的二元一次方程是；
（3）如图（4），若并排n个正方形内接于抛物线y=-x（x-2），则每个正方形的边长a_n满足的二元一次方程是；