
题目列表(包括答案和解析)
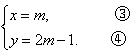
| A.十岁通五经通:通晓 | B.自蜀至长安,道未振振:振作 |
| C.白益傲放益:更加 | D.白时卧庐山,辟为僚佐辟:征召,被…聘用 |
| A.因以命之衡因上疏陈事 | B.以所业投贺知章何面目以归汉 |
| C.遂荐于玄宗而君幸于赵王 | D.白长笑而去天苍苍而高也 |
| A.②③④ | B.③④⑤ | C.①③④ | D.②③⑤ |
| A.李母梦见太白金星而生下李白,所以李白的名字中有“白”字。李白天赋过人,才华横溢。 |
| B.贺知章很欣赏李白的诗才,感叹他是遭贬的仙人。李白后经贺知章的推荐,担任翰林供奉。 |
| C.在朝廷上下,李白都表现出放荡不羁的个性,这说明李白是个决不“摧眉折腰事权贵”的人。 |
| D.郭子仪曾有恩于李白。后来,李白受牵连下狱,郭子仪又请求用自己的官爵来赎免李白的死罪。 |
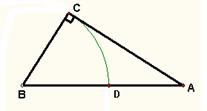
古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如![]() (a>0,b>0)的方程的图解法是:如图,以
(a>0,b>0)的方程的图解法是:如图,以![]() 和b为两直角边做Rt△ABC,再在斜边上截取BD=
和b为两直角边做Rt△ABC,再在斜边上截取BD=![]() ,则AD的长就是所求方程的解。
,则AD的长就是所求方程的解。
(1)请用含字母a、b的代数式表示AD的长。
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com