【图形变换的探究与猜想】
从特殊到一般,从全等到相似;求证线段的数量关系或位置关系.关键是第一问的全等的证明,发现全等的三角形,一般是利用ASA完成证明,从而得到需要证明的相似三角形(利用两边对应成比例且夹角相等).
例:正方形ABCD,E为直线AB上任意一点,DF⊥DE交直线BC于点F,直线EF、AC交于点H,连接DH.
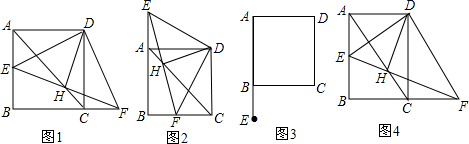
(1)①如图1,当点E在边AB上时,判断线段DH与线段EF之间的数量关系和位置关系;
②如图2,当点E在边AB的反向延长线上时,判断线段DH与线段EF之间的数量关系和位置关系;写出你的结论并从①、②中任选一个证明;
(2)如图3,若点E在AB边的延长线上,其它条件不变,完成图3,判断线段DH与线段EF之间的数量关系和位置关系,直接写出你的结论,不需要证明;
(3)如图4,若将图1中的正方形ABCD改为矩形ABCD为正方形,且AB=kAD,其它条件不变,判断线段DH与线段EF之间的数量关系和位置关系,直接写出结论,不需要证明.

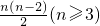 条对角线
条对角线 180°(n≥3),它有
180°(n≥3),它有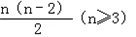 条对角线
条对角线