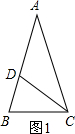
如图，已知△ABC中，AB=AC，∠A=36°．仿照图(1)请你再设计两种不同的方法将△ABC分割成3个小三角形，使得每个小三角形都是等腰三角形(图(2)(3)供画图用)，作图工具不限，只标出所得的每个三角形三个内角的度数，不写画法和证明．

如图，已知△ABC中，AB=AC，∠A=36°．仿照图(1)请你再设计两种不同的方法将△ABC分割成3个小三角形，使得每个小三角形都是等腰三角形(图(2)(3)供画图用)，作图工具不限，只标出所得的每个三角形三个内角的度数，不写画法和证明．

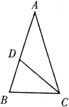
我们知道：将一条线段AB分割成大小两条线段AC、CB，若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比，即

CB

AC

=

AC

AB

=

5 -1

2

=0.61803398874989．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
（1）如图1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分线CD交腰AB于点D，请你说明D为腰AB的黄金分割点的理由．
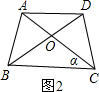
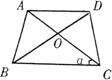
（2）若腰和上底相等，对角线和下底相等的等腰梯形叫作黄金梯形，其对角线的交点为对角线的黄金分割点．如图2，AD‖BC，AB=AD=DC，AC=BD=BC，试说明O为AC的黄金分割点．
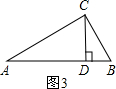
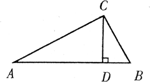
（3）如图3，在Rt△ABC中，∠ACB=90°，CD为斜边AB上的高，∠A、∠B、∠ACB的对边分别为a、b、c．若D是AB的黄金分割点，那么a、b、c之间的数量关系是什么并证明你的结论．