乘法公式的探究及应用.

1.如左图，可以求出阴影部分的面积是            （写成两数平方差的形式）；  

2.如右图，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是             ，长是            ，面积是              （写成多项式乘法的形式）

3.比较左、右两图的阴影部分面积，可以得到乘法公式           （用式子表达）

4.应用所得的公式计算：

乘法公式的探究及应用.
【小题1】如左图，可以求出阴影部分的面积是            （写成两数平方差的形式）；  
【小题2】如右图，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是             ，长是            ，面积是              （写成多项式乘法的形式）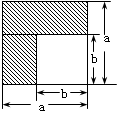

【小题3】比较左、右两图的阴影部分面积，可以得到乘法公式           （用式子表达）
【小题4】应用所得的公式计算：