如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90⁰，∠B=∠E=30⁰.

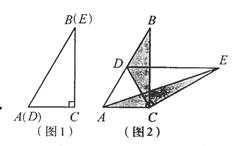
（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转。当点D恰好落在BC边上时，填空：线段DE与AC的位置关系是     ；

②设△BDC的面积为S₁，△AEC的面积为S₂。则S₁与S₂的数量关系是     。

（2）猜想论证

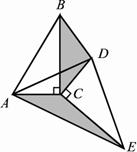
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S₁与S₂的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想。

（3）拓展探究

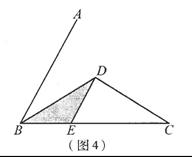
已知∠ABC=60⁰，点D是其角平分线上一点，BD=CD=4，OE∥AB交BC于点E（如图4），若在射线BA上存在点F，使S_△DCF =S_△BDC,请直接写出相应的BF的长

如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90º,∠B=∠E=30º.

（1）操作发现

如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：

线段DE与AC的位置关系是          ；

设△BDC的面积为S₁，△AEC的面积为S₂，则S₁与S₂的数量关系是          ，证明你的结论；

猜想论证

当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S₁与S₂的数量关系仍然成立，并尝试分别作出了△BDC和△AE中BC，CE边上的高，请你证明小明的猜想．

如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.

(1)操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：

①线段DE与AC的位置关系是    ；

②设△BDC的面积为S₁，△AEC的面积为S₂，那么S₁，S₂之间的数量关系是    ；

(2)猜想论证

当△DEC绕点C旋转到图3所示的位置时，小明猜想(1)中S₁与S₂的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想；

(3)拓展探究

       已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.

若在射线BA上存在点F，使S_△DCF=S_△BDE，请直接写出相应的BF的长.