阅读下面的文言文,完成小题。(19分)
张南垣传 【清】吴伟业
张南垣名涟,南垣其字,华亭人,徙秀州,又为秀州人。少学画,好写人像,兼通山水,遂以其意垒石,故他艺不甚著,其垒石最工,在他人为之莫能及也。
君为人肥而短黑,性滑稽,好举里巷谐媟为抚掌之资。或陈语旧闻,反以此受人啁弄,亦不顾也。与人交,好谈人之善,不择高下,能安异同,以此游于江南诸郡者五十余年。自华亭、秀州外,于白门、于金沙、于海虞、于娄东、于鹿城,所过必数月。其所为园,则李工部之横云、虞观察之予园、王奉常之乐郊、钱宗伯之拂水、吴吏部之竹亭为最著。经营粉本,高下浓淡,早有成法。初立土山,树石未添,岩壑已具,随皴随改,烟云渲染,补入无痕。即一花一竹,疏密欹斜,妙得俯仰。山未成,先思著屋,屋未就,又思其中之所施设,窗棂几榻,不事雕饰,雅合自然。主人解事者,君不受促迫,次第结构,其或任情自用,不得已骫骳曲折,后有过者,辄叹息曰:“此必非南垣意也。”
君为此技既久,土石草树,咸能识其性情。每创手之日,乱石林立,或卧或倚,君踌躇四顾,正势侧峰,横支竖理,皆默识在心,借成众手。常高坐一室,与客谈笑,呼役夫曰:“某树下某石可置某处。”目不转视,手不再指,若金在冶,不假斧凿。甚至施竿结顶,悬而下缒,尺寸勿爽,观者以此服其能矣。人有学其术者,以为曲折变化,此君生平之所长,尽其心力以求仿佛,初见或似,久观辄非。
而君独规模大势使人于数日之内寻丈之间落落难合及其既就则天堕地出得未曾有。曾于友人斋前作荆、关老笔,对峙平墄(台阶的梯级),已过五寻,不作一折,忽于其颠,将数石盘互得势,则全体飞动,苍然不群。
所谓他人为之莫能及者,盖以此也。
君有四子,能传父术。晚岁辞涿鹿相国之聘,遣其仲子行,退老于鸳湖之侧,结庐三楹。余过之谓余曰:“
自吾以此术游江以南也,数十年来,名园别墅易其故主者,比比多矣。荡于兵火,没于荆榛,奇花异石,他人辇取以去,吾仍为之营置者,辄数见焉。吾惧石之不足留吾名,而欲得子文以传之也。”余曰:“柳宗元为《梓人传》,谓有得于经国治民之旨。今观张君之术,虽庖丁解牛,公输刻鹄,无以复过,其艺而合于道者欤!君子不作无益,穿池筑台,《春秋》所戒,而王公贵人,歌舞般乐,侈欲伤财,独此为耳目之观,稍有合于清净。且张君因深就高,合自然,惜人力,此学愚公之术而变焉者也,其可传也已。”作《张南垣传》。(有删节)
注:①谐媟(xiè):诙谐不恭敬。②粉本:建筑物的草图。③皴(cūn):中国画技法之一,涂出物体纹理或阴阳向背。④骫骳(wěibèi):曲折委婉。
【小题1】对下列句子中划线词语的解释,不正确的一项是( )(3分)
| A.好举里巷谐媟以为抚掌之资抚掌:拍手,表示高兴。 |
| B.经营粉本,高下浓淡经营:经度营造 |
| C.不事雕饰,雅合自然雅:文雅 |
| D.尺寸勿爽爽:差错 |
【小题2】下列各组句子中,划线词的意义和用法相同的一组是( )(3分)
| A.尽其心力以求仿佛赵王岂以一璧之故欺秦邪 |
| B.则李工部之横云之二虫,又何知 |
| C.辄数见焉吴之民方痛心焉 |
| D.与人交,好谈人之善始可与言《诗》已矣 |
【小题3】下列对原文的赏析不正确的一项是( )(3分)
| A.本文所记述的张南垣尤擅长垒石造山,具有山水画的意境,构思巧妙,师法自然。 |
| B.本文例举了张南垣所建造园林的代表作及其建造过程,说明他的建造风格,并指出他的技艺符合园林建造的规律。 |
| C.本文还描写了张南垣的外貌性格,因为生得黑而矮胖,又喜欢拿街头巷尾荒唐不经的传说作为谈笑的资料,所以他自己也常常被人调笑耍弄,但他从不与人计较。 |
| D.全文语言流畅工丽,结构严谨,写人状物,如在目前。 |
【小题4】用“∕”给文中画波浪线的部分断句。(3分)
而 君 独 规 模 大 势 使 人 于 数 日 之 内 寻 丈 之 间 落 落 难 合 及 其 既 就 则 天 堕 地 出 得 未 曾 有
【小题5】把文中画线的句子译成现代汉语。(7分)
(1)所谓他人为之莫能及者,盖以此也。(3分)
(2)自吾以此术游江以南也,数十年来,名园别墅易其故主者,比比多矣。(4分)


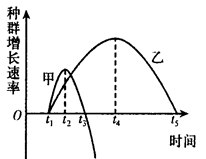
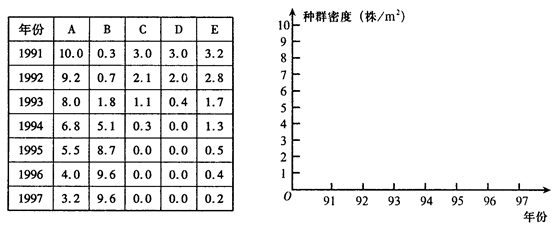
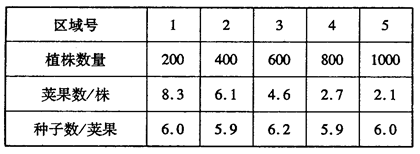
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?