
题目列表(包括答案和解析)
 个单位长度的速度沿AB方向运动,点Q从点C出发以每秒2个单位长度的速度沿CD方向运动,P、Q两点同时出发,当点P到达到点B时停止运动,点Q也随之停止.过点P作PE⊥OA于点E,PF⊥OB于点F,得到矩形PEOF.以点Q为直角顶点向下作等腰直角三角形QMN,斜边MN∥OB,且MN=QC.设运动时间为t(单位:秒).
个单位长度的速度沿AB方向运动,点Q从点C出发以每秒2个单位长度的速度沿CD方向运动,P、Q两点同时出发,当点P到达到点B时停止运动,点Q也随之停止.过点P作PE⊥OA于点E,PF⊥OB于点F,得到矩形PEOF.以点Q为直角顶点向下作等腰直角三角形QMN,斜边MN∥OB,且MN=QC.设运动时间为t(单位:秒).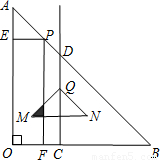
 个单位长度的速度沿AB方向运动,点Q从点C出发以每秒2个单位长度的速度沿CD方向运动,P、Q两点同时出发,当点P到达到点B时停止运动,点Q也随之停止.过点P作PE⊥OA于点E,PF⊥OB于点F,得到矩形PEOF.以点Q为直角顶点向下作等腰直角三角形QMN,斜边MN∥OB,且MN=QC.设运动时间为t(单位:秒).
个单位长度的速度沿AB方向运动,点Q从点C出发以每秒2个单位长度的速度沿CD方向运动,P、Q两点同时出发,当点P到达到点B时停止运动,点Q也随之停止.过点P作PE⊥OA于点E,PF⊥OB于点F,得到矩形PEOF.以点Q为直角顶点向下作等腰直角三角形QMN,斜边MN∥OB,且MN=QC.设运动时间为t(单位:秒).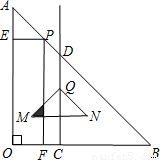
如图,在等腰梯形ABCD中,AD∥BC,AC、BD相交于点O,则图中全等三角形
共有……………………………………………………………………………………( )
(A)1对 (B)3对 (C)2对 (D)4对

【提示】以AB和CD为对应边的两个三角形.
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
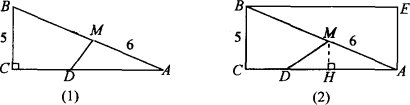
(1)动点D在边AC上运动,且与点A、C均不重合,设CD=x.
①设△ABC与△ADM的面积之比为y,求y与x之间的函数关系式(写出自变量x的取值范围);
②当x取何值时,△ADM是等腰三角形?写出你的理由.
(2)如图(2),以图(1)中的BC、CA为一组邻边的矩形ACBE中,动点D在矩形边上运动一周,能使△ADM是以∠AMD为顶角的等腰三角形共有多少个(直接写出结果,不要求说明理由)?
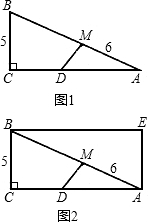 如图1,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
如图1,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com