
题目列表(包括答案和解析)
| c |
| x |
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
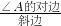 ,cosA=
,cosA=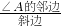 ,tanA=
,tanA=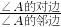 ,cotA=
,cotA=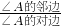

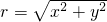 (r总是正的),然后把角α的三角函数规定为:
(r总是正的),然后把角α的三角函数规定为: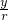 ,cosα=
,cosα=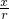 ,tanα=
,tanα=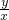 ,cotα=
,cotα=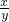
 ),且cosα=
),且cosα=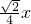 ,则tanα______;
,则tanα______;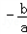 、x1x2=
、x1x2= ,这个定理叫做韦达定理.如:x1、x2是方程x2+2x﹣1=0的两个根,则x1+x2=﹣2、x1x2=﹣1.若x1、x2是一元两次方程2x2+mx﹣2m+1=0的两个实数根.
,这个定理叫做韦达定理.如:x1、x2是方程x2+2x﹣1=0的两个根,则x1+x2=﹣2、x1x2=﹣1.若x1、x2是一元两次方程2x2+mx﹣2m+1=0的两个实数根.| b |
| a |
| c |
| a |
| 1 |
| 2 |
| x | 2 1 |
| x | 2 2 |
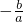 、x1•x2=
、x1•x2= ,这个定理叫做韦达定理. 如:x1、x2是方程x2+2x-1=0的两个实数根,则x1+x2=-2、x1•x2=-1. 若x1,x2是方程
,这个定理叫做韦达定理. 如:x1、x2是方程x2+2x-1=0的两个实数根,则x1+x2=-2、x1•x2=-1. 若x1,x2是方程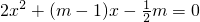 的两个实根.试求:
的两个实根.试求: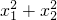 的值(用含有m的代数式表示);
的值(用含有m的代数式表示);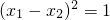 ,试求m的值.
,试求m的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com