阅读下面文言文(每小题3分,共12分)
李白传
白,字太白,山东人。母梦长庚星而诞,因以命之。十岁通五经。自梦笔头生花,后天才赡逸。喜纵横,击剑为任侠,轻财好施。更客任城,与孔巢父、韩准、裴政、张叔明、陶沔居徂徕山中,日沉饮,号“竹溪六逸”。
天宝初,自蜀至长安,道未振,以所业投贺知章,读至《蜀道难》,叹曰:“子,谪仙人也。”乃解金龟换酒,终日相乐。遂荐于玄宗。召见金銮殿,论时事。因奏颂一篇。帝喜,赐食,亲为调羹,诏供奉翰林。尝大醉上前,草诏,使高力士脱靴。力士耻之,摘其《清平调》中飞燕事,以激怒贵妃。
帝每欲与官,妃辄阻之。白益傲放,与贺知章、李适之、汝阳王琎、崔宗之、苏晋、张旭、焦遂为“饮酒八仙人”。恳求还山。赐黄金,诏放归。
白浮游四方,欲登华山,乘醉跨驴经县治,
宰不知,怒,引至庭下曰:“汝何人,敢无礼?”白供状不书姓名,曰:“曾令龙巾拭吐,御手调羹,贵妃捧砚,力士脱靴。天子门前,尚容走马;华阴县里,不得骑驴?”宰惊愧,拜谢曰:“不知翰林至此。”白长笑而去。尝乘舟,与崔宗之自采石至金陵,著宫锦袍坐,旁若无人。禄山反,明皇在蜀,永王璘节度东南。白时卧庐山,辟为僚佐。璘起兵反,白逃还彭泽。璘败,累系浔阳狱。初,白游并洲,见郭子仪,奇之,曾救其死罪。至是,郭子仪请官以赎,诏长流夜郎。
白晚节好黄、老,度牛渚矶,乘酒捉月,沉水中。初,悦谢家青山,今墓在焉。
(节选自人教版普通高中新课程语文读本④)
【小题1】对下列句子中加点的词语解释不正确的一项是( )
| A.十岁通五经通:通晓 | B.自蜀至长安,道未振振:振作 |
| C.白益傲放益:更加 | D.白时卧庐山,辟为僚佐辟:征召,被…聘用 |
【小题2】下列各组句子中,加点词的意义和用法相同的一组是( )
| A.因以命之衡因上疏陈事 | B.以所业投贺知章何面目以归汉 |
| C.遂荐于玄宗而君幸于赵王 | D.白长笑而去天苍苍而高也 |
【小题3】能体现李白“傲放”个性的一组是( )
①自梦笔头生花,后天才赡逸。②以所业投贺知章,读至《蜀道难》,叹曰:“子,谪仙人也。”③尝大醉上前,草诏,使高力士脱靴。④白浮游四方,欲登华山,乘醉跨驴经县。⑤著宫锦袍坐,旁若无人。
【小题4】下列对原文有关内容的分析与概括,不正确的一项是( )
| A.李母梦见太白金星而生下李白,所以李白的名字中有“白”字。李白天赋过人,才华横溢。 |
| B.贺知章很欣赏李白的诗才,感叹他是遭贬的仙人。李白后经贺知章的推荐,担任翰林供奉。 |
| C.在朝廷上下,李白都表现出放荡不羁的个性,这说明李白是个决不“摧眉折腰事权贵”的人。 |
| D.郭子仪曾有恩于李白。后来,李白受牵连下狱,郭子仪又请求用自己的官爵来赎免李白的死罪。 |
【小题5】将文中画横线的句子翻译成现代汉语。(6分)
(1)帝每欲与官,妃辄阻之。(3分)译文:
(2)宰不知,怒,引至庭下曰。(3分)译文:

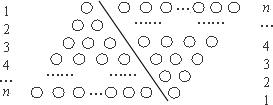
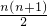 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=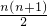 .
.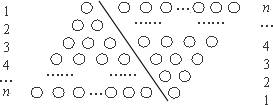
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=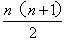 。
。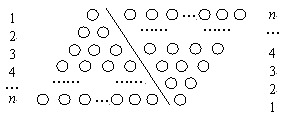
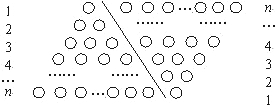 并利用图形做必要的推理说明)
并利用图形做必要的推理说明)