
题目列表(包括答案和解析)
若a、b、c均为整数,且∣a-b∣3+∣c-a∣2=1,
求∣a-c∣+∣c-b∣+∣b-a∣的值(8分)
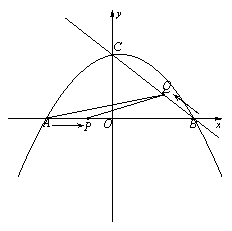
如图,抛物线y=-![]() x2+bx+c交x轴于A、B两点,交y轴于点C,且抛物线的对称轴为直线x=1,设∠ABC=α,且cosα=
x2+bx+c交x轴于A、B两点,交y轴于点C,且抛物线的对称轴为直线x=1,设∠ABC=α,且cosα=![]() .
.
(1)求这条抛物线的函数关系式;
(2)动点P从点A出发,沿A→B→C方向,向点C运动;动点Q从点B出发,沿射线BC方向运动.若P、Q两点同时出发,运动速度均为1个单位长度/秒,当点P到达点C时,整个运动随之结束,设运动时间为t秒.
①试求△APQ的面积S与t之间的函数关系式,并指出自变量t的取值范围;
②在运动过程中,是否存在这样的t的值,使得△APQ是以AP为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.
(Ⅰ)如图,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;

(Ⅱ)如图,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2;
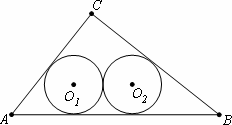
(Ⅲ)如图,当n大于2的正整数时,若半径rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、BC相切,⊙On与BC、AB相切,⊙O1、⊙O2、⊙O3、…、⊙On-1均与AB边相切,求rn.

附加题:已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.
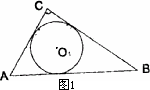
(1)如图1,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
(2)如图2,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2;
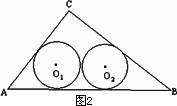
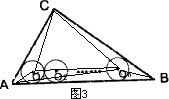
(3)如图3,当n是大于2的正整数时,若半径为rn的n个等圆⊙O1、⊙O2、……、⊙ON依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O2、⊙O3、……、⊙On-1均与AB边相切,求rn.
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
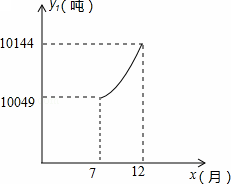
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y2=ax2+c(a≠0).其图象如图所示.1至6月,污水厂处理每吨污水的费用:z1(元)与月份x之间满足函数关系式:z1=![]() x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=
x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=![]() x-
x-![]() x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出y1,y2与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a-30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.(参考数据:![]() ≈15.2,
≈15.2,![]() ≈20.5,
≈20.5,![]() ≈28.4)
≈28.4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com