
题目列表(包括答案和解析)
| 8 | & | # | x | -5 | 2 | … |
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| | | | | | | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | | | | | |
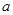 、
、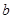 、
、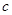 、
、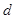 又有什么规律呢?请用含的
又有什么规律呢?请用含的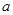 、
、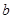 、
、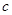 、
、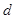 等式表示: 。
等式表示: 。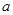 、
、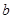 、
、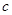 、
、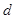 四个数之间的大小关系是
四个数之间的大小关系是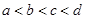 ,
,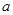 、
、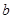 、
、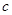 、
、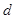 整数)
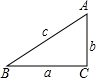
整数)在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示.
(1)如图(1),在△ABC中,∠A=2∠B,且∠A=60°.
求证:a2=b(b+c);
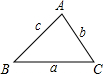
(2)如图(2),如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.本题第(Ⅰ)问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角△ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?并证明你的结论;

(3)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数.
在如图所示的2005年1月份日历中,
|
星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
30 |
31 |
|
|
|
|
|
(1)用一个长方形的方框圈出任意3×3个数,如果从左下角到右上角的“对角线”上的3个数字的和为39,那么这9个数的和为 ;
(2)这个长方形的方框圈出的9个数的和能为216吗?答 :(填“能”或“不能”);
(3)如果任意选择如上的阴影部分,那么其中的四个数 、
、 、
、 、
、 又有什么规律呢?请用含的
又有什么规律呢?请用含的 、
、 、
、 、
、 等式表示:
。
等式表示:
。
(其中 、
、 、
、 、
、 四个数之间的大小关系是
四个数之间的大小关系是 ,
, 、
、 、
、 、
、 整数)
整数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com