如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性.

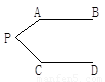
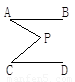
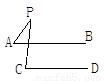
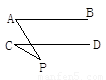
结论（1）____________________________；（2）____________________________；

（3）____________________________；（4）____________________________；

选择结论________，说明理由是什么.

如图，已知AB∥CD，分别探究下面四个图形中∠P和∠A、∠C的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性．

结论（1）______（2）______（3）______（4）______．我选择结论______．说明理由．

如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，请从你所得四个关系中选出任意一个，说明你探究的结论的正确性．

结论：（1）______；（2）______；（3）______；（4）______．

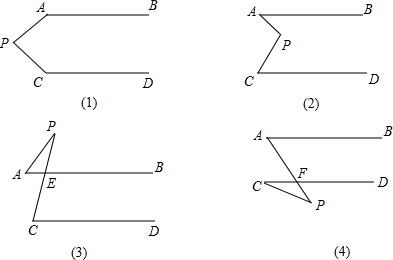
如图，在下列矩形ABCD中，已知：AB＝a，BC＝b（a＜b），假定顶点在矩形边上的菱形叫做矩形的内接菱形，现给出（Ⅰ）、（Ⅱ）、（Ⅲ）三个命题：

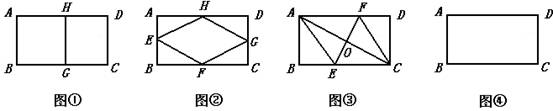
命题（Ⅰ）：图①中，若AH＝BG＝AB，则四边形ABGH是矩形ABCD的内接菱形；

命题（Ⅱ）：图②中，若点E、F、G和H分别是AB、BC、CD和DE的中点，则四边形EFGH是矩形ABCD的内接菱形；

命题（Ⅲ）：图③中，若EF垂直平分对角线AC，变BC于点E，交AD于点F，交AC于点O，则四边形AECF是矩形ABCD的内接菱形.

请解决下列问题：

1.命题（Ⅰ）、（Ⅱ）、（Ⅲ）都是真命题吗？请你在其中选择一个，并证明它是真命题或假命题；

2.画出一个新的矩形内接菱形（即与你在（1）中所确认的，但不全等的内接菱形）.

3.试探究比较图①，②，③中的四边形ABGH、EFGH、AECF的面积大小关系