解方程组

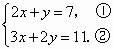
解：由①，得y＝7－2x．③

把③代入②，得3x＋2(7－2x)＝11，x＝3．

把x＝3代入③，得y＝7－2×3，y＝1．

所以

上面解二元一次方程组的基本思想是“消元”，也就是要消去其中一个未知数，把二元一次方程组转化成一元一次方程．这里的消元方法是，从一个方程中求出某一个未知数的表达式，再把它“代入”另一个方程，进行求解，这种方法叫做________消元法，简称________．

我们在解决数学问题时，经常采用“转化”(或“化归”)的思想方法，把待解决的问题，通过某种转化过程，归结到一类已解决或比较容易解决的问题．

譬如，在学习了一元一次方程的解法以后，进一步研究二元一次方程组的解法时，我们通常采用“消元”的方法，把二元一次方程组转化为一元一次方程；再譬如，在学习了三角形内角和定理以后，进一步研究多边形的内角和问题时，我们通常借助添加辅助线，把多边形转化为三角形，从而解决问题．

问题提出：如何把一个正方形分割成n(n≥9)个小正方形？

为解决上面问题，我们先来研究两种简单的“基本分割法”．

基本分割法1：如图①，把一个正方形分割成4个小正方形，即在原来1个正方形的基础上增加了3个正方形．

基本分割法2：如图②，把一个正方形分割成6个小正方形，即在原来1个正方形的基础上增加了5个正方形．

问题解决：有了上述两种“基本分割法”后，我们就可以把一个正方形分割成n(n≥9)个小正方形．

(1)把一个正方形分割成9个小正方形．

一种方法：如图③，把图①中的任意1个小正方形按“基本分割法2”进行分割，就可增加5个小正方形，从而分割成4＋5＝9(个)小正方形．

另一种方法：如图④，把图②中的任意1个小正方形按“基本分割法1”进行分割，就可增加3个小正方形，从而分割成6＋3＝9(个)小正方形．

(2)把一个正方形分割成10个小正方形．

方法：如图⑤，把图①中的任意2个小正方形按“基本分割法1”进行分割，就可增加3×2个小正方形，从而分割成4＋3×2＝10(个)小正方形．

(3)请你参照上述分割方法，把图⑥给出的正方形分割成11个小正方形(用钢笔或圆珠笔画出草图即可，不用说明分割方法)

(4)把一个正方形分割成n(n≥9)个小正方形．

方法：通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形，再在此基础上每使用1次“基本分割法1”，就可增加3个小正方形，从而把一个正方形分割成12个、13个、14个小正方形，依次类推，即可把一个正方形分割成n(n≥9)个小正方形．

从上面的分法可以看出，解决问题的关键就是找到两种基本分割法，然后通过这两种基本分割法或其组合把正方形分割成n(n≥9)个小正方形．

类比应用：仿照上面的方法，我们可以把一个正三角形分割成n(n≥9)个小正三角形．

(1)基本分割法1：把一个正三角形分割成4个小正三角形(请你在图a中画出草图)．

(2)基本分割法2：把一个正三角形分割成6个小正三角形(请你在图b中画出草图)．

(3)分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形(用钢笔或圆珠笔画出草图即可，不用说明分割方法)

(4)请你写出把一个正三角形分割成n(n≥9)个小正三角形的分割方法(只写出分割方法，不用画图)．