
题目列表(包括答案和解析)
在日常生活和生产实践中有不少问题是可以用一次函数来解决的.一般地,用一次函数解决实际问题的基本步骤是:(1)先判断两个变量之间是否构成_________关系;(2)求得函数解析式;(3)利用函数解析式或其图象解决实际问题.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
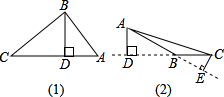 cm,求CB的长.
cm,求CB的长.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com