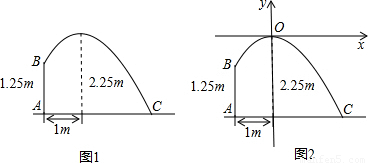
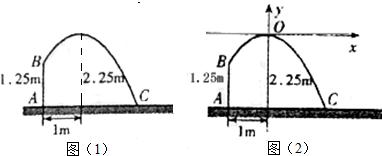
如图1,某灌溉设备的喷头B高出地面1.25m,喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m,试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式.
学生小龙在解答图1所示的问题时,具体解答如下:
①以水流的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图
2所示的平面直角坐标系;
②设抛物线水流对应的二次函数关系式为y=ax
2;
③根据题意可得B点与x轴的距离为1m,故B点的坐标为(-1,1);
④代入y=ax
2得-1=a•1,所以a=-1;
⑤所以抛物线水流对应的二次函数关系式为y=-x
2.
数学老师看了小龙的解题过程说:“小龙的解答是错误的”.
(1)请指出小龙的解答从第______步开始出现错误,错误的原因是什么?
(2)请你写出完整的正确解答过程.