
题目列表(包括答案和解析)
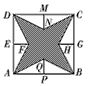
如图:正方形的边长为 a。①用代数式表示阴影的面积;
②若 a=2cm 时,求阴影的面积(结果保留π)。



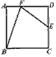
 与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,
与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2, 与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OAnBnCn与扇形OAnCn之间的阴影部分面积为Sn。
与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OAnBnCn与扇形OAnCn之间的阴影部分面积为Sn。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com