
题目列表(包括答案和解析)
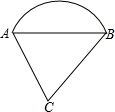 (2011•河西区模拟)如图,是一个由弓形和三角形组成的组合图形,若取
(2011•河西区模拟)如图,是一个由弓形和三角形组成的组合图形,若取 | AB |
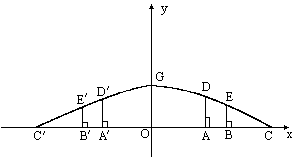
如图,某市一处十字路口立交桥的截面是由抛物线和两个对称的三角形组成.其中抛物线![]() 可以用y=-
可以用y=-![]() x2+8表示,线段CD和
x2+8表示,线段CD和![]() 为两段对称的上桥斜坡,其坡度为1∶4.AD和
为两段对称的上桥斜坡,其坡度为1∶4.AD和![]() 是两侧的支柱,OA和
是两侧的支柱,OA和![]() 为两个方向的汽车通行区,宽都为15米.
为两个方向的汽车通行区,宽都为15米.
(1)求![]() 的长;
的长;
(2)BE和![]() 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和![]() 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和![]() 的宽;
的宽;
(3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米,今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米,那么这辆运货汽车能否从OA(或![]() )区域安全通过?请说明理由.
)区域安全通过?请说明理由.
我国著名数学家华罗庚曾说过:撌?毙问鄙僦惫郏?紊偈?蹦讶胛ⅲ皇?谓岷习侔愫茫?衾敕旨彝蚴滦輸.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.

(1
)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)(2
)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明) 25、线段、角、三角形、和圆都是几何研究的基本图形,请用这些图形设计表现客观事物的图案,每幅图可以由一种图形组成,也可以由两种或三种图案组成,但总数不得超过三个,并且为每幅图案命名,命名要求与画面相符(如图的示例)(不少于2幅)
25、线段、角、三角形、和圆都是几何研究的基本图形,请用这些图形设计表现客观事物的图案,每幅图可以由一种图形组成,也可以由两种或三种图案组成,但总数不得超过三个,并且为每幅图案命名,命名要求与画面相符(如图的示例)(不少于2幅)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com