
题目列表(包括答案和解析)
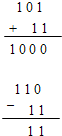 28、我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数为:
28、我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数为:我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数为:

(101)2=1×22+0×21+1=4+0+1=5;(1011)2=1×23+0×22+1×21+1=11;
两个二进制数可以相加减,相加减时,将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似,应用“逢二进一”、“退一还二”的运算法则,如: (101)2+(11)2=(1000)2;(110)2+(11)2=(11)2,用竖式运算如右侧所示.(12分)
(1)按此方式,将二进制(1001)2换算成十进制数的结果是 ▲ .
(2)计算:(10101)2+(111)2= ▲ (结果仍用二进制数表示);
(110010)2-(1111)2= ▲ (结果用十进制数表示).
我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数为:

(101)2=1×22+0×21+1=4+0+1=5;(1011)2=1×23+0×22+1×21+1=11;
两个二进制数可以相加减,相加减时,将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似,应用“逢二进一”、“退一还二”的运算法则,如: (101)2+(11)2=(1000)2;(110)2+(11)2=(11)2,用竖式运算如右侧所示.(12分)
(1)按此方式,将二进制(1001)2换算成十进制数的结果是 ▲ .
(2)计算:(10101)2+(111)2= ▲ (结果仍用二进制数表示);
(110010)2-(1111)2= ▲ (结果用十进制数表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com