
题目列表(包括答案和解析)
 点F.
点F. |
| AE |
 |
| DE |
 |
| AD |
 如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E.求证:
如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E.求证: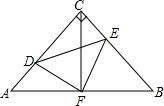 如图,在等腰Rt△ABC中,∠ACB=90°,F是AB边上的中点,点D,E分别在AC,BC边上运动,且始终保持AD=CE,连接DE,DF,EF.探究:
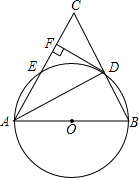
如图,在等腰Rt△ABC中,∠ACB=90°,F是AB边上的中点,点D,E分别在AC,BC边上运动,且始终保持AD=CE,连接DE,DF,EF.探究: (9分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为点F.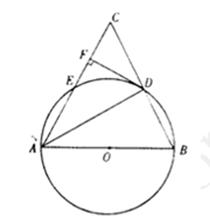
(1)求证:DF是⊙O的切线;
(2)若弧AE=弧DE,DF=2,求弧AD的长.
如图,在△ABC中,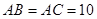 cm,
cm,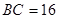 cm,
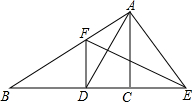
cm,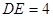 cm,动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达C时运动停止,过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为
cm,动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达C时运动停止,过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为 秒(
秒(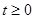 )
)
(1)直接写出用含 的代数式表示线段BE、EF的长;
的代数式表示线段BE、EF的长;
(2)在这个动动过程中,△DEF能否为等腰三角形?若能,请求出 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com