
题目列表(包括答案和解析)
一个三角形两边中点的连线叫做这个三角形的中位线.我们可以看到图1三角形的三条中位线把这个三角形分成了4个小的三角形,而且这些小的三角形都是全等的.
把三条边都分成三等份,再按图2将分点连起来,可以看到整个三角形被分成了9个小的三角形,而且这些小的三角形也都是全等的.
我们还可以把3条边都分成4等份,再似图1、图2那样将分点连起来,可以看到整个三角形被分成了一个个更小的全等的三角形.
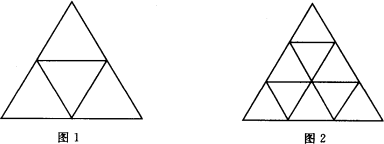
现在请你和你的同学一起参与如下的探究活动:
1.数一数图1、图2中的点、线段和全等三角形的个数,用一张表记录下来;
2.再把3条边都分成4等份,似图1、图2那样将分点连起来,数一数这时的点、线段和全等三角形的个数,也记录在相应的表格中;
3.仔细分析所得到的一些数据,相互交流讨论,想一想其中有什么关系;
4.继续把3条边都分成5,6…等份,似图1、图2那样将分点连起来,数一数这时的点、线段和全等三角形的个数,看看与你的猜想是否符合;
5.将三角形换成四边形,探究一下这时有什么规律.
 23、已知以下基本事实:①对顶角相等;②一条直线截两条平行直线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④全等三角形的对应边、对应角分别相等.
23、已知以下基本事实:①对顶角相等;②一条直线截两条平行直线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④全等三角形的对应边、对应角分别相等.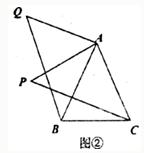 26、
26、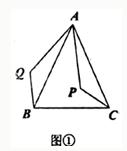 复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com