
题目列表(包括答案和解析)
 21、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
21、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.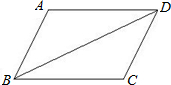 21、如图所示,已知AD=BC,AB=DC,试判断∠A与∠B的关系,下面是小颖同学的推导过程,你能说明小颖的每一步的理由吗?
21、如图所示,已知AD=BC,AB=DC,试判断∠A与∠B的关系,下面是小颖同学的推导过程,你能说明小颖的每一步的理由吗?如图所示,已知:⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
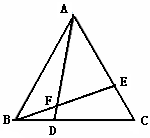
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿BEA相似吗?说说你的理由.
(3)等式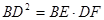 成立吗?请说明理由.
成立吗?请说明理由.
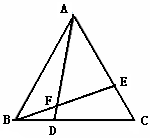
 成立吗?请说明理由.
成立吗?请说明理由.如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).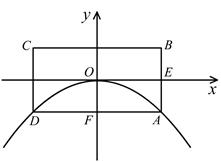
(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com