27、阅读下面的材料并解答问题.
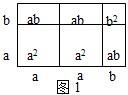
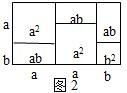
图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系.例如完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如(2a+b)(a+b)=2a
2+3ab+b
2就可以用图1或图2等图形的面积表示:
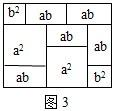
(1)请写出图3所表示的代数恒等式:
(a+2b)(2a+b)=2a2+5ab+2b2
解决问题:
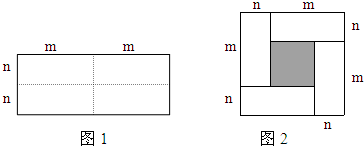
某钢铁加工厂现有足够的2×2,3×3的正方形和2×3的矩形下脚料A、B、C(如图所示),现从中各选取若干个下脚料焊接成不同的图形,请你在下面给出的方格纸中,按下列要求分别画出一种示意图(说明:下面给出的方格纸中,每个小正方形的边长均为1,拼出的图形,要求每两个图片之间既无缝隙,也无重叠,画图必须保留拼较的痕迹)
A、

B、

C、

(2)选取A型4块,B型两种图片1块,C型图片4块,在下面的图2中拼成一个正方形;
利用面积法去解,如图所示.

(3)选取A型3块,B型两种图片1块,C型图片若干块,在下面的图3中拼成一个长方形.





 B、
B、 C、
C、


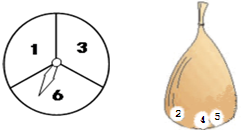 分小于7,则宁宁获胜,这个游戏公平吗?为什么?
分小于7,则宁宁获胜,这个游戏公平吗?为什么?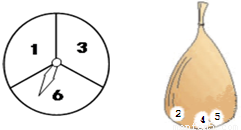
 分小于7,则宁宁获胜,这个游戏公平吗?为什么?
分小于7,则宁宁获胜,这个游戏公平吗?为什么?