钟面数字问题
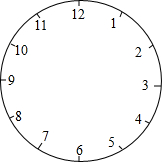
如图,钟面上有1,2,3,…,11,12这12个数字.
(1)试在某些数的前面添加负号,使它们的代数和为零
(2)能否改变钟面上的数,比如只剩下6个偶数,仍按第(1)小题的要求来做?
[思路探究]
(1)我们先试着选定任意几个数字,在其前面添加负号,如
-12-11-10+9+8+7+6-5+4+3+2+1-2.
这当然不是我们要的答案,但我们可以将其调整,比如改变1前面的符号,得
-12-11-10+9+8+7+6-5+4+3+2-1-0.
用这种方法当然可以得到许多答案,但我们并不满足.我们希望寻找其中的规律,使我们能找到更多的解答.我们发现:
在调整符号的过程中,若将一个正数变号,12个数的代数和就减少这个正数的两倍;若将一个负数变号,12个数的代数和就增加这个负数的绝对值的两倍.
要使12个数的代数和为零,其中正数的和的绝对值必须与负数的和的绝对值相等,均为12个数之和的-半,即等于39.
由此,我们只要找到几个和为39的数,将这些数添上负号即可.
由于最大3个数之和为33<39,因此必须再添上一个6才有解答,所以添加负号的数至少要有4个.同理可知,添加负号的数最多不超过8个.
根据以上规律,就能在很短的时间内得到许多解答,但是要写出所有解答,还必须把答案作适当的分类.本题共有124个解答,亲爱的读者,你能写出这124个解答来吗?
(2)因为2+4+6+8+10+12-42,它的一半为21,而奇数不可能通过偶数求和得到,所以只剩下6个偶数时,不能按第(1)小题的要求来做.

 钟面数字问题
钟面数字问题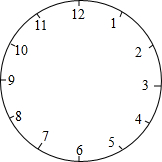 钟面数字问题
钟面数字问题