
题目列表(包括答案和解析)
 15、如图所示,一位运动员在离篮下4米水平距离处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5米时,球达到最大高度3.5米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面
15、如图所示,一位运动员在离篮下4米水平距离处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5米时,球达到最大高度3.5米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面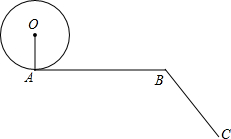 一位小朋友在一轨道上滚动一个半径为10cm的圆盘,如图所示,其中∠ABC=120°,AB=60cm,BC=40cm,该小朋友将圆盘从A点滚动到C点,则其圆心所经过的路线的长度为
一位小朋友在一轨道上滚动一个半径为10cm的圆盘,如图所示,其中∠ABC=120°,AB=60cm,BC=40cm,该小朋友将圆盘从A点滚动到C点,则其圆心所经过的路线的长度为
| 32 | 3 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com