
题目列表(包括答案和解析)
阅读: 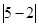 表示5与2差的绝对值,也可理解为5与2两数在数轴上所
表示5与2差的绝对值,也可理解为5与2两数在数轴上所
对应的两点之间的距离; 可以看做
可以看做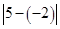 ,表示5与-2的差的绝对值,也
,表示5与-2的差的绝对值,也
可理解为5与-2两数在数轴上所对应的两点之间的距离.
探索:
1.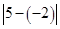 =___________
=___________
2.利用数轴,找出所有符合条件的整数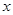 ,使
,使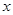 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7
3.由以上探索猜想,对于任何有理数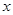 ,
,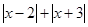 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最
小值;如果没有,说明理由
阅读: ![]() 表示5与2差的绝对值,也可理解为5与2两数在数轴上所
表示5与2差的绝对值,也可理解为5与2两数在数轴上所
对应的两点之间的距离;![]() 可以看做
可以看做![]() ,表示5与-2的差的绝对值,也
,表示5与-2的差的绝对值,也
可理解为5与-2两数在数轴上所对应的两点之间的距离.
探索:
1.![]() =___________
=___________
2.利用数轴,找出所有符合条件的整数![]() ,使
,使![]() 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7
3.由以上探索猜想,对于任何有理数![]() ,
,![]() 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最
小值;如果没有,说明理由
| 6 |
| 5 |
| 8 |
| 7 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com