练习册

  • 练习册
  • 试题
    (三).运用举例 变式练习 例1 比较-4与-|-3|的大小? 例2 已知a＞b＞0.比较a.-a.b.-b的大小? 例3 比较-与-的大小? 课堂练习 1.?比较下列每对数的大小: 与,|2|与,-与, 与? 2.?比较下列每对数的大小: -与-,-与-,-与-,-与-? 【查看更多】

     

    题目列表(包括答案和解析)

    如图a，P为△ABC内任一点，试证明∠BPC=∠ABP＋∠ACP＋∠A．

    　　　　　　  

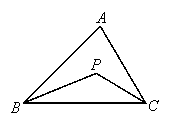
    变式一　如图，若点P为△ABC两角∠ABC和∠ACB的平分线的交点，则∠BPC和∠A有怎样的关系?

    变式二　如图，“变式一”已知不动，另补上“若点Q是它们外角平分线的交点”，则∠BPC和∠Q有何关系?

    变式三　一个零件的形状如图所示，按规定∠A应等于90°，∠B、∠C分别是21°和32°．检验工人量得∠BDC=148°．就断定这个零件不合格，这是为什么?

    查看答案和解析>>

    （教材变式题）用加减法解方程组
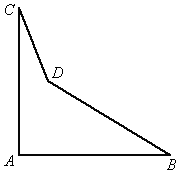
    8x+7y=-20①
    8x-5y=16②
    解题步骤如下：
    （1）①-②，得12y=-36，y=-3
    （2）①×5+②×7，得96x=12，x=
    1
    8
    ，下列说法正确的是（　　）
    A、步骤（1），（2）都不对
    B、步骤（1），（2）都对
    C、此题不适宜用加减法
    D、加减法不能用两次

    查看答案和解析>>

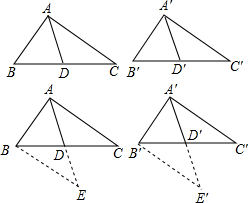    （2013•莒南县一模）【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（无需证明）
    【拓展变式】小明很顺利的完成了上面的练习后，又进一步对该命题进行了发散思维，把原命题中的一些条件进行了变换，得到了如下三个不同的命题：
    （1）如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．
    （2）如果两个三角形有两条边和第三边上的高对应相等，那么这两个三角形全等．
    （3）如果两个三角形有两条边和夹角的平分线对应相等，那么这两个三角形全等．
    【探索新知】小明对这三个命题，无法判断其命题的真假，于是他向老师求教．数学老师对命题（1）做出了一些指导，请你帮助小明完成下面的解答过程．
    已知：如图，AB=A′B′，AD=A′D′，AD是BC边上的中线，A′D′是B′C′边上的中线，求证：△ABC≌△A′B′C′，
    证明：如图，延长AD至E使AD=DE，连接BE，延长A′D′至E′使A′D′=D′E′，连接B′E′．
    【合作学习】对于命题（2）、（3），你能帮助小明判断命题的真假吗？如果是真命题，请给完整的证明，如果是假命题，在下面的空白处做出解答．（要求：画出图形，说明理由．）

    查看答案和解析>>

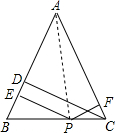    精英家教网【老题重现】
    求证：等腰三角形底边上任意一点到两腰的距离和等于一腰上的高．
    已知：△ABC中，AB=AC，点P是BC边上任意一点，PE⊥AB于E，PF⊥AC于F，CD是AB边上的高线．
    求证：PE+PF=CD
    证明：连接AP，
    ∵S△ABP+S△ACP=S△ABC
    ∴
    AB×PE
    2
    +
    AC×PF
    2
    =
    AB×CD
    2

    ∵AB=AC
    ∴PE+PF=CD

    【变式应用】
    请利用“类比”和“化归”两种方法解答下面问题：
    求证：等边三角形内上任意一点到三边的距离和等于一边上的高．
    已知：点P是等边△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AH是BC边上的高线．精英家教网
    求证：PD+PE+PF=AH
    证明：
    方法（一）类比：通过类比上题的思路和方法，模仿上题的“面积法”解决本题．
    连接AP，BP，CP
    方法（二）化归：如图，通过MN在等边△ABC中构造符合“老题”规律的等边△AMN，化“新题”为“老题”，直接利用“老题重现”的结论解决问题．
    过点P作MN∥BC，交AB于M，交AC于N，交AH于G．

    【提炼运用】
    已知：点P是等边△ABC内任意一点，设到三边的距离分别为a、b、c，且使得以a、b、c为边能够构成三角形．
    请在图中画出满足条件的点P一切可能的位置，并对这些位置加以说明．
    精英家教网

    查看答案和解析>>

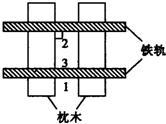    60、（教材变式题）“垂直于同一条直线的两直线平行”，运用这一性质可以说明铺设铁轨互相平行的道理．
    如图所示，已知∠2是直角，再度量出∠1或∠3就会知道铁轨平行不平行．
    [解答]
    方案一：若量得∠3=90°，结合∠2情况，说明理由；
    方案二：若量得∠1=90°，结合∠2情况，说明理由．

    查看答案和解析>>


    同步练习册答案