练习册

  • 练习册
  • 试题
    如图1所示,下列说法不正确的是( )毛 A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段 (3) 【查看更多】

     

    题目列表(包括答案和解析)

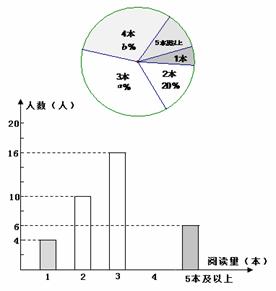
     某学校为了解八年级学生的课外阅读情况，钟老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图7所示，但不完整的统计图.根据图示信息，解答下列问题：

    （1）求被抽查学生人数及课外阅读量的众数；

    （2）求扇形统计图汇总的、值；

    （3）将条形统计图补充完整；

    （4）若规定：假期阅读3本以上（含3本）课外书籍者为完成假期作业，据此估计该校600名学生中，完成假期作业的有多少人？

    查看答案和解析>>

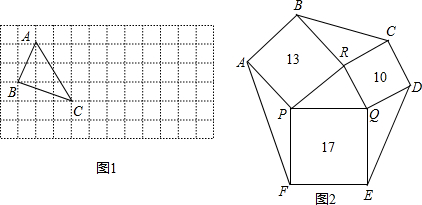
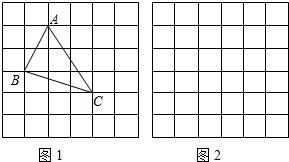    精英家教网“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
    例：在△ABC中，AB、BC、AC三边长分别是
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．
    小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：S△ABC=3×3-
    1
    2
    ×3×1-
    1
    2
    ×2×1-
    1
    2
    ×3×2=
    7
    2

    思维拓展：已知△ABC的边长分别为
    		5a
    、2
    		2a
    、
    		17a
    (a＞0)    ，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．

    查看答案和解析>>

    问题背景：在△ABC中，AB、BC、AC三边的长分别为
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶精英家教网点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
    （1）请你将△ABC的面积直接填写在横线上．
     

    （2）画△DEF，DE、EF、DF三边的长分别为
    		2
    、
    		8
    、
    		10

    ①判断三角形的形状，说明理由．
    ②求这个三角形的面积．

    查看答案和解析>>

    在△ABC中，AB、BC、AC三边的长分别为
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
    （1）△ABC的面积为：
     
    ；
    （2）若△DEF三边的长分别为
    		5
    、2
    		2
    、
    		17
    ，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；
    （3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．
    精英家教网

    查看答案和解析>>

    在△ABC中，AB、BC、AC三边的长分别为
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
    （1）△ABC的面积为：
    3.5
    3.5
    ．
    （2）若△DEF三边的长分别为
    		5
    、
    		8
    、
    		17
    ，请在图2的正方形网格中画出相应的△DEF，并利用构图法求出它的面积为
    3
    3
    ．
    （3）如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．试探究EP与FQ之间的数量关系，并证明你的结论．
    （4）如图4，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13m2、25m2、36m2，则六边形花坛ABCDEF的面积是
    110
    110
    m2．

    查看答案和解析>>


    同步练习册答案