练习册

  • 练习册
  • 试题
    如图:△ABC中.∠B=2∠C.AD是BC边上的高.求证:AB+BD=DC. 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在△ABC中，AD是BC边上的高，tanB=cos∠DAC。
    （1）证明：AC=BD；
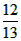    （2）若sinC=，BC=18，求AD的长。

    查看答案和解析>>

    如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA=，特别地，当点D、E重合时，规定：λA=0，另外，对λB、λC作类似的规定。
    （1）如图2，在△ABC中，∠C=90°，∠A=30°，求λA、λC；
    （2）在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且λA=2，面积也为2；
    （3）判断下列三个命题的真假（真命题打“√”，假命题打“×”）：
    ①若△ABC中λA＜1，则△ABC为锐角三角形；
    ②若△ABC中λA=1，则△ABC为锐角三角形；
    ③若△ABC中λA＞1，则△ABC为锐角三角形。

    查看答案和解析>>

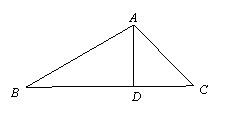    如图，已知：在△ABC中，AD是BC边上的高，∠B=30°，∠C=45°，，求AD的长。

    查看答案和解析>>

    如图，已知AD是△ABC的中线，∠ADC＝45°，把△ABC沿AD对折，点C落在点E的位置，连接BE，若BC＝6cm。

    （1）求BE的长；

    （2）当AD=4cm时，求四边形BDAE的面积。

    【解析】（1）由折叠可知：△ADC≌△ADE，∠EDC=2∠ADC=90°，ED=DC，又BD=DC，△BDE是等腰直角三角形，可求BE长；

    （2）由（1）知，∠BED=45°，∠EDA=45°，∴四边形BDAE是梯形，已知上底AD=4，下底BE=3 2，为求梯形高，过D作DF⊥BE于点F，DF实际上就是等腰直角三角形BDE斜边上的高，可求长度．

     

    查看答案和解析>>

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h。张红的作法是：（1）作线段BC=a；（2）作线段BC的垂直平分线MN，MN与BC相交于点D；（3）在直线MN上截取线段h；（4）连结AB，AC，△ABC为所求的等腰三角形。上述作法的四个步骤中，有错误的一步你认为是

    [     ]

    A、（1）
    B、（2）
    C、（3）
    D、（4）

    查看答案和解析>>


    同步练习册答案