从2开始，连续的偶数相加，它们的和的情况如下表：
加数m的个数   和(S)
1　———————————→2＝1×2
2　————————→2＋4＝6＝2×3
3　——————→2＋4＋6＝12＝3×4
4　————→2＋4＋6＋8＝20＝4×5
5　——→2＋4＋6＋8＋10＝30＝5×6
(1)按这个规律，当m＝6时，和为_______；
(2)从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：
__________________________________________．
(3)应用上述公式计算：
①2＋4＋6＋…＋200  　　 ②202＋204＋206＋…＋300

（12＇）如图，某水库拦水坝的迎水坡AD的坡度i=3：7，坝顶宽8米，坝高6米， cosB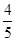＝，求：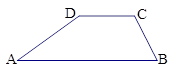

　（1）背水坡BC的长。
（2）坝底宽AB。
（3）水坝截面的面积S。

先阅读下列材料，然后解答问题：
材料1　从3张不同的卡片中选取2张排成一列，有6种不同的排法，抽象成数学问题就是从3个不同元素中选取2个元素的排列，排列数记为A₃²＝3×2＝6.
一般地，从n个不同元素中选取m个元素的排列数记作A_n^m，
A_n^m＝n(n－1)(n－2)…(n－m＋1)(m≤n)．
例：从5个不同元素中选3个元素排成一列的排列数为：A₅³＝5×4×3＝60.
材料2　从3张不同的卡片中选取2张，有3种不同的选法，抽象成数学问题就是从3个元素中选取2个元素的组合，组合数记为C₃²＝＝3.
一般地，从n个不同元素中选取m个元素的组合数记作C_n^m，
C_n^m＝ (m≤n)．
例：从6个不同元素中选3个元素的组合数为：
C₆³＝＝20.
问：(1)从7个人中选取4人排成一排，有多少种不同的排法？
(2)从某个学习小组8人中选取3人参加活动，有多少种不同的选法？

从2开始，连续的偶数相加，它们的和的情况如下表：

    加数m的个数    和(S)

    1　———————————→2＝1×2

    2　————————→2＋4＝6＝2×3

    3　——————→2＋4＋6＝12＝3×4

    4　————→2＋4＋6＋8＝20＝4×5

    5　——→2＋4＋6＋8＋10＝30＝5×6

  (1)按这个规律，当m＝6时，和为_______；

  (2)从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：

 __________________________________________．

  (3)应用上述公式计算：

   ①2＋4＋6＋…＋200   　　 ②202＋204＋206＋…＋300