
题目列表(包括答案和解析)
国家主管部门规定:从2008年6月1日起,各商家禁止向消费者免费提供一次性塑料购物袋.为了了解巴中市市民对此规定的看法,对本市年龄在16-65岁之间的居民,进行了400个随机访问抽样调查,并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图.

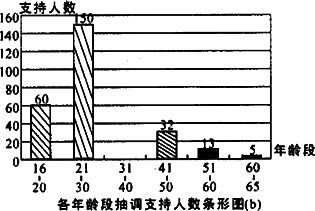
根据上图提供的信息回答下列问题:
(1)被调查的居民中,人数最多的年龄段是________岁.
(2)已知被调查的400人中有83%的人对此规定表示支持,请你求出31-40岁年龄段的满意人数,并补全图b.
(3)比较21-30岁和41-50岁这两个年龄段对此规定的支持率的高低(四舍五入到1%,注:某年龄段的支持率![]() ).
).
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如撏?资?莸某朔ǚㄔ驍的学习过程是利用有理数的乘方概念和乘法结合律,由撎厥鈹到撘话銛进行抽象概括的:![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
![]()
![]()
我们亦知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1
)请你根据上面的材料归纳出(2
)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:撊-(3
)如图,在
某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额-生产成本-投资)为z(万元).
(1)试写出y与x之间的函数关系式(不必写出x的取值范围).
(2)试写出z与x之间的函数关系式(不必写出x的取值范围).
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划在第一年按年获利最大确定的销售单价进行销售;第二年年获利不低于1130万元.请你借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
2012年5月30日,在“六一国际儿童节”来临之际,某初级中学开展了向贫困地区“希望小学”捐赠图书活动.全校1000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图24-1所示. 学校为了了解各年级捐赠图书情况,按照图-1的比例从各年级中随机抽查了共200名学生,进行捐赠图书情况的统计,绘制成如图24-2的频数分布直方图.
根据以上信息回答下列问题:
(1)本次调查的样本是 ▲ ;
(2)从图-2中,我们可以看出人均捐赠图书最多的是___▲____年级;
(3)随机抽查的200名学生中九年级学生共捐赠图书多少册?
(4)估计全校共捐赠图书多少册?
2012年5月30日,在“六一国际儿童节”来临之际,某初级中学开展了向贫困地区“希望小学”捐赠图书活动.全校1000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图24-1所示. 学校为了了解各年级捐赠图书情况,按照图-1的比例从各年级中随机抽查了共200名学生,进行捐赠图书情况的统计,绘制成如图24-2的频数分布直方图.
根据以上信息回答下列问题:
(1)本次调查的样本是 ▲ ;
(2)从图-2中,我们可以看出人均捐赠图书最多的是___▲____年级;
(3)随机抽查的200名学生中九年级学生共捐赠图书多少册?

(4)估计全校共捐赠图书多少册?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com