
题目列表(包括答案和解析)
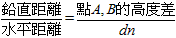 ;
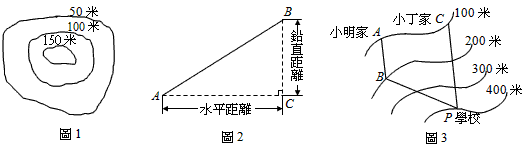
;
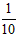 到
到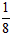 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在
之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在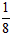 到
到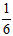 之间时,小明和小丁步行的平均速度均约为1米/秒)
之间时,小明和小丁步行的平均速度均约为1米/秒)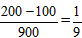 ;
;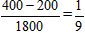 ;
;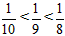 ,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。因为____,所以小丁在路段CP上步行的平均速度约为____米/秒,斜坡AB的距离=
,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。因为____,所以小丁在路段CP上步行的平均速度约为____米/秒,斜坡AB的距离=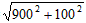 ≈906(米),
≈906(米),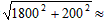 1811(米),斜坡CP的距离=
1811(米),斜坡CP的距离=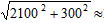 2121(米),
2121(米),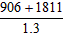 =2090(秒)。
=2090(秒)。
小强和爸爸上山游玩,两人距地面的高度y(米)与小强登山时间x(分)之间的函数图象分别如图中折线OAC和线段DE所示,根据函数图象进行以下探究:
信息读取:(1)爸爸登山的速度是每分钟 米;(2)请解释图中点B的实际意义;
图象理解:
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(4)计算并填空:m= ;
问题解决:
(5)若小强提速后,他登山的速度是爸爸速度的3倍,问小强登山多长时间时开始提速?此时小强距地面的高度是多少米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com