练习册

  • 练习册
  • 试题
    15．解:原式＝ 提示:把二次项3x2分解成x与3x(二次项一般都只分解成正因数).常数项10可分成1×10＝-1×.其中只有11x=x×5+3x×2. 说明:十字相乘法是二次三项式分解因式的一种常用方法.特别是当二次项的系数不是1的时候.给我们的分解带来麻烦.这里主要就是讲讲这类情况.分解时.把二次项.常数项分别分解成两个数的积.并使它们交叉相乘的积的各等于一次项.需要注意的是:⑴如果常数项是正数.则应把它分解成两个同号的因数.若一次项是正.则同正号,若一次项是负.则应同负号.⑵如果常数项是负数.则应把它分解成两个异号的因数.交叉相乘所得的积中.绝对值大的与一次项的符号相同(若一次项是正.则交叉相乘所得的积中.绝对值大的就是正号,若一次项是负.则交叉相乘所得的积中.绝对值大的就是负号). ax c 二次项 常数项 bx d adx+bcx=x 一次项 ab x2+ 【查看更多】

     

    题目列表(包括答案和解析)

    阅读下面的解题过程并填空：

    计算：(－15)÷×6．

    解：原式＝(－15)÷×6(第一步)

    ＝(－15)÷(－25)(第二步)

    ＝．(第三步)

    (1)上面解题过程中有两处错误，第一处错误是第________步，错误原因是________；第二处错误是第________步，错误原因是________．

    (2)正确的结果是________．

    查看答案和解析>>

    阅读下列因式分解的过程，再回答所提出的问题：

    1＋x＋x(x+1)＋x(x＋1)2=(1＋x)[1＋x＋x(1＋x)]

                      =(1＋x)2[1＋x]

                      =(1＋x)3

    (1)上述分解因式的方法是               法，共应用了       　　次.

    (2)若分解1＋x＋x(x＋1)＋x(x＋1)2＋…＋x(x＋1)2010，则需要应用上述方法     　　次，分解因式后的结果是　　　　　　　　.

    (3)请用以上的方法分解因式：1＋x＋x(x＋1)＋x(x＋1)2＋…＋x(x＋1)n(n为正整数)，必须有简要的过程。

    (3)解：原式＝(1＋x)[1＋x＋x(1＋x)…x(1＋x)(n－1)]

         ＝(1＋x)2[1＋x＋x(1＋x)…x(1＋x)(n－2)]

                  …

           ＝ (1＋x)n

    查看答案和解析>>

    阅读下列解答过程是否正确，若有错，指出错因，并改正过来．

    计算－23÷(－)×(－10)＋(－1)2008．

    解：原式＝－8÷1＋1＝－8＋1＝－7．

    查看答案和解析>>

    阅读下列解题过程，请回答是否不错误，如果有，请指出错误的一步，并出

    正确的解答过程。

    化简

    解：原式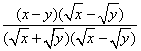＝　　　　　　　　　　　　　　　　　　　　 ①

    ＝　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

    ＝－。　　　　　　　　　　　　　　　　　　　　　　　　　　　　  ③

     

    查看答案和解析>>

    计算：

    (1)(2＋3)(2－3)

    解：原式＝

    (2)(－)－(＋)＋(π－1)0

    解：原式＝

    (3)[(1＋)(x－4＋)－3]÷(－1)

    解：原式＝

    查看答案和解析>>


    同步练习册答案