练习册

  • 练习册
  • 试题
    如图7-1-3所示.已知AD.BE.CF分别是△ABC的高.中线和角平分线.则∠ =∠ =90°, = =,∠ =∠ =∠ . 图7-1-3 解析:直接依据三角形的高.中线.角平分线的定义可得. 答案:ADB ADC AE CE AC ACF BCF ACB 【查看更多】

     

    题目列表(包括答案和解析)

    如图，已知四边形ABCD是平行四边形，若点E、F分别在边BC、AD上，连接AE、CF，请再从下列三个备选条件中，选择添加一个恰当的条件．使四边形AECF是平行四边形，并予以证明，
    备选条件：AE=CF，BE=DF，∠AEB=∠CFD，
    我选择添加的条件是：______．
    （注意：请根据所选择的条件在答题卡相应试题的图中，画出符合要求的示意图，并加以证明）

    查看答案和解析>>

    如图，已知四边形ABCD是平行四边形，若点E、F分别在边BC、AD上，连接AE、CF，请再从下列三个备选条件中，选择添加一个恰当的条件．使四边形AECF是平行四边形，并予以证明，
    备选条件：AE=CF，BE=DF，∠AEB=∠CFD，
    我选择添加的条件是：________．
    （注意：请根据所选择的条件在答题卡相应试题的图中，画出符合要求的示意图，并加以证明）

    查看答案和解析>>

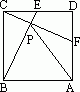
    已知，如图所示，在正方形ABCD中，E、F分别是CD、AD的中点，BE与CF相交于点P，若AP＝18．求正方形ABCD的面积．

    查看答案和解析>>

    （1）已知AD是∠BAC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E、F，BD=CD，求证：∠B= ∠C．
    （2）如图所示，在△ABC中，D是BC的中点，DE⊥AB于点E，D⊥AC于点F，且BE=CF，求证：AD平分∠BAC。

    查看答案和解析>>

    用尺规作图，并回答问题

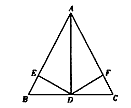
    如图所示，已知钝角△ABC．

    (1)分别作△ABC三边上的高AD、BE、CF；

    (2)观察AD、BE、CF所在的直线，三条直线是否相交于一点？

    ________________________________________________

    (3)思考：三角形三条高所在直线的交点位置，随三角形的形状各异(锐角三角形、直角三角形、钝角三角形)而有何不同？

    ________________________________________________

    查看答案和解析>>


    同步练习册答案