
题目列表(包括答案和解析)
如下图所示,抛物线y=-(x-m)2的顶点为A,直线l:y=![]() x-
x-![]() m与y轴的交点为B,其中m>0.
m与y轴的交点为B,其中m>0.

(1)写出抛物线对称轴及顶点A的坐标(用含m的代数式表示);
(2)证明点A在直线l上,并求∠OAB的度数;
(3)动点Q在抛物线对称轴上,抛物线上是否存在点P,使以P,Q,A为顶点的三角形与△OAB全等?若存在,求出m的值,并写出所有符合上述条件的P点坐标;若不存在,说明理由.
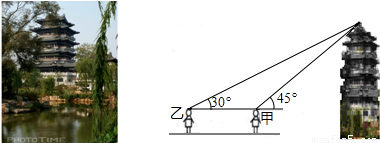
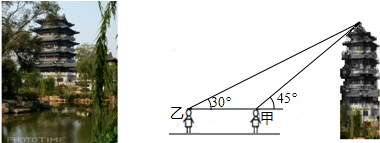 假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:
假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话: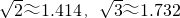 )
) )
)
如下图,抛物线![]() (其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到
(其中m,n为常数且m>n)与y轴正半轴交于A点,它的对称轴交x轴正半轴于C点,抛物线的顶点为P,Rt△ABC的直角顶点B在对称轴上,当它绕点C按顺时针方向旋转90°得到![]() .
.

(1)写出点![]() 的坐标(用含m,n的式子表示);
的坐标(用含m,n的式子表示);
(2)若直线![]() 交y轴于E点,求证:线段
交y轴于E点,求证:线段![]() 与
与![]() 互相平分;
互相平分;
(3)若点![]() 在抛物线上且Rt△ABC的面积为1时,请求出抛物线的解析式并判断在抛物线的对称轴上是否存在点D,使
在抛物线上且Rt△ABC的面积为1时,请求出抛物线的解析式并判断在抛物线的对称轴上是否存在点D,使![]() 为等腰三角形?若存在,请直接写出所有符合条件的D点坐标;若不存在,请说明理由.
为等腰三角形?若存在,请直接写出所有符合条件的D点坐标;若不存在,请说明理由.
[注:抛物线y=ax2+bx+c顶点坐标是![]() ]
]
 如图所示:抛物线y=x2-2x-3交坐标轴于A、B、C三点,D是抛物线的顶点,M在对称轴上,P在坐标轴上.以下结论:
如图所示:抛物线y=x2-2x-3交坐标轴于A、B、C三点,D是抛物线的顶点,M在对称轴上,P在坐标轴上.以下结论: ;
; ;
;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com